Introduction

Distributed parallel computing takes place on a network of computers, where there is no shared memory across computers. Some kind of message passing is usually used to share data between processes. The main advantage distributed parallel computing has over shared memory computing (GPU or CPU) is that you have access to much more random access memory, which enables you to solve data-intensive problems that don't fit in the memory of a single computer.

It's worth learning about this subject from a parallel computing course and/or from a textbook, such as my Elements of Parallel Computing [1]. These notes are only meant to present some of the features of Julia's support for distributed parallel computing, and not a complete course in the subject, and focus on lower level details of the programming model. Julia offers higher level abstractions, such as the DistributedArrays package.

These notes use the word count task to illustrate distributed parallel computing. We will count the occurence of words in a 5.8 MB file of text from Project Gutenberg, containing the complete works of Shakespeare. The lines of the text file are read into an array of strings using the following function:

function readLines(textfile)
    lines = String[]
    open(textfile) do f
        for line in eachline(f)
            push!(lines, line)
        end
    end
    lines
end

readLines (generic function with 1 method)

Our task is to count the occurences of each word in the text. First, the strings are split into words and converted to lower case, using a list of common delimiters:

function readWords(lines::Vector{String})
    words = String[]
    for line in lines
        lineWords = split(line, (' ','\n','\t','-','.',',',':','_','"',';','!','?'); keepempty=false)
        map(w -> push!(words, lowercase(w)), lineWords)
    end
    words
end

readWords (generic function with 1 method)

This results in an array of words. The next phase is to count the words, using a dictionary to store the results:

function wordCount(words::Vector{String})
    wordcounts = Dict{String,Int64}()
    for word in words
        wordcounts[word]=get(wordcounts, word, 0) + 1
    end
    wordcounts
end

wordCount (generic function with 1 method)

The last argument in the call to get means that if word is not in the wordcounts dictionary then it will return a value of zero. Now we can put all the pieces together and time each of the three subtasks:

function wordCount(textfile::String)
    @time lines = readLines(textfile)
    @time words = readWords(lines)
    @time wordcounts = wordCount(words)
end

wordCount (generic function with 2 methods)

In the following we call wordCount twice, looking at the last result to avoid including the cost of compilation:

wcs = wordCount("shakespeareComplete.txt")

0.034810 seconds (139.53 k allocations: 11.451 MiB)
  0.449124 seconds (3.50 M allocations: 215.489 MiB, 18.36% gc time)
  0.093240 seconds (30 allocations: 1.419 MiB)

wcs = wordCount("shakespeareComplete.txt");

0.128883 seconds (139.53 k allocations: 11.451 MiB, 64.72% gc time)
  0.552960 seconds (3.50 M allocations: 215.489 MiB, 44.21% gc time)
  0.095355 seconds (30 allocations: 1.419 MiB)
Dict{String, Int64} with 33084 entries:
  "baleful"      => 7
  "oblique"      => 2
  "profess'd"    => 3
  "dial's"       => 1
  "frowning"     => 15
  "gout"         => 7
  "propositions" => 1
  "back'st"      => 1
  "henry"        => 604
  "work'st"      => 1
  "228"          => 1
  "tameness"     => 2
  "entomb"       => 3
  "rises"        => 16
  "sun’s"        => 2
  "unwholesome"  => 10
  "greatness’"   => 1
  "paul’s"       => 1
  "redresses"    => 2
  ⋮              => ⋮

By far the most time is spent in the splitting of lines into words. The least time is spent in reading the file, which is a good thing since this is tricky to parallelize. We can parallelize the other two subtasks by decomposing the lines array into chunks that will be assigned to worker processes.

Julia's Distributed Parallel Programming Model

Distributed parallel programming in Julia is done using a master-worker model with message passing. In the master-worker model the master process maintains a queue of data that needs processing, coordinates execution of the tasks by the worker processes, and gathers the results. In Julia processes can be added interactively, using addprocs(n), which creates n worker processes having ids 2 to n+1 (the master, the current process, has id = 1). By default this will launch the processes on cores of the local machine. It's also possible to launch worker processes across a cluster (see parallel computing manual). Another way to create worker processes is to launch Julia with the -p option, such as julia -p 4 to create 4 workers.

Execution of tasks on the worker processes is done using one of a group of methods that perform remote execution of functions. We'll use one of them here, remote_do; for others see Julia's distributed computing documentation. Communication between processes can be done using RemoteChannels. The return value from a remote function call can also be fetched, but we'll leave an example of this until part 2. Interprocess communication is one-sided, in that data is put in a RemoteChannel or or taken from a RemoteChannel. A RemoteChannel is a handle to a Channel, which is stored on the master or on a worker. A Channel can be viewed as a queue, or pipe, that is written to on one end and read from the other end.

In our parallel word count solution we'll use two RemoteChannels: one to store chunks of the lines array, and one to store the dictionaries produced by each worker. Both are stored on the master node:

using Distributed
function wordCountPar(textfile::String, chunks=nworkers())
    lines = readLines(textfile)
    inputC = RemoteChannel(()->Channel{Vector{String}}(chunks))
    outputC = RemoteChannel(()->Channel{Dict{String,Int64}}(nworkers()))
    storeChunks!(inputC, lines, chunks)
    for p in workers()
        remote_do(wordCountParHelper!, p, inputC, outputC)
    end
    mergeDicts(outputC)
end

wordCountPar (generic function with 2 methods)

The RemoteChanel constructor includes an argument to specify the length of the channel. The input channel can contain chunks String vectors and the output channel can contain nworkers() (the number of workers) dictionaries. The default number of chunks is one per worker, but as we'll see, more can be used to help balance the load of the workers. In the loop above the workers() function returns an array of worker ids. Worker execution is launched using the remote_do method, which asynchronously launches the function in the first parameter on the process indicated in the second parameter; the arguments to the function make up the remaining arguments. Asynchronous execution means the calls to remote_do return immediately, and do not wait for the remote execution to complete. Finally, the resulting dictionaries from each worker are merged. Let's look at the functions used to populate the input channel and merge the data in the output channel. The decomposition of the array of lines is done using the function:

function storeChunks!(rchannel, a, chunks)
    n = length(a)
    for i in 1:chunks
        lo = ((i-1)*n)÷chunks + 1
        hi = (i*n)÷chunks
        put!(rchannel, a[lo:hi])
    end
    nothing
end

storeChunks! (generic function with 1 method)

which puts contiguous chunks of an array into rchannel. The dictionaries produced by each worker are merged together by the function:

function mergeDicts(rchannel)
    wordcounts = take!(rchannel)
    for p in workers()[2:nworkers()]
        wcs = take!(rchannel)
        merge!(+, wordcounts, wcs)
    end
    wordcounts
end

mergeDicts (generic function with 1 method)

Note that the take! method blocks until there is data in the channel. Therefore mergeDicts will start merging once dictionaries arrive in the output channel. The remaining function needed is wordCountParHelper:

@everywhere function wordCountParHelper!(inputC, outputC)
    lines = Vector{String}
    try
        lines = take!(inputC)
    catch e # remote channel is closed, so no work to do
        wordcounts = Dict{String,Int64}()
        put!(outputC, wordcounts) # send empty dict to output
        return
    end
    words = readWords(lines)
    wordcounts = wordCount(words)
    while true
        if !isready(inputC)
            close(inputC) # won't cause error if already closed
            break
        end
        try
            lines = take!(inputC)
        catch e # remote channel is closed
            break
        end
        words = readWords(lines)
        wcs = wordCount(words)
        merge!(+, wordcounts, wcs)
    end
    put!(outputC, wordcounts)
    nothing
end

This function gives the instructions that each worker will execute. The default number of chunks is the same as the number of workers, but more chunks can help balance the load. The workers take chunks from the input RemoteChannel (which implies communication between master and worker processes) and count the words in each chunk. The take() is wrapped in a try-catch block in case other workers have completed the work and closed the input RemoteChannel. The workers keep processing chunks, merging results from each chunk into a single dictionary. When there are no more chunks to process, each worker puts its dictionary in the output RemoteChannel (once again, implying worker-master communication). A worker knows there are no more chunks when the channel is empty (using isready()). The first worker to encounter an empty input RemoteChannel closes it (close() does nothing if the channel is already closed). If another worker tries to take from the closed channel then the try-catch block will ensure it stops processing chunks. Finally, note the @everywhere macro in front of the wordCountParHelper!(). This is needed to load the function on every worker. The @everywhere macro needs to be added to the signature of the readWords(), and wordCount() functions as well, since they will be called by workers.

Running wordCountPar("shakespeareComplete.txt") on 2 worker processes gives the following timing results, when run on a dual-processor 24 core Intel® Xeon® Platinum 8168 using @btime from BenchmarkTools on Julia 1.5.0:

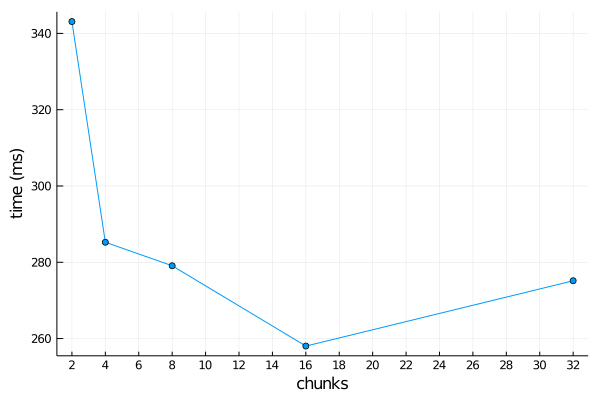
In comparison, the sequential word count takes 496 ms. There's a signficant increase in performance when the number of chunks is increased from one per worker. Even though we have close to an equal number of lines for each worker to process, each line won't have the same number of words, and the total number of distinct words may vary across chunks, so the workload won't be balanced across workers. Increasing the number of chunks allows a worker that finishes early to do more work.

Here's the speedup for our parallel word count for 2,4,8,16, and 32 workers on two processors (total of 48 cores):

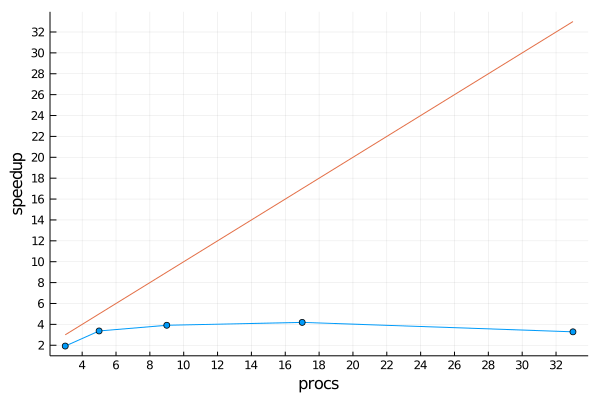
Note that we've calculated the speedup based on the total number of processes (nworkers()+1). For each point we've found the number of chunks that led to the fastest time, as we did above for 2 workers. The speedup is reasonable for 2 and 4 workers, but quickly reaches a plateau. This is expected as the parallel overhead, including setting up chunks and communication with workers, increases with the number of workers, while each worker's workload decreases.

Summary

Julia's distributed parallel programming model uses the master-worker model. The master makes remote calls to execute functions on the workers. We used here the asynchronous remote_do methods, which is one of several similar methods, including remotecall, remotecall_fetch, and remotecall_wait. For more details, see the documentation. Here we used RemoteChannels on the master to communicate with the workers. These channels can also be stored on worker processes, so it's possible to have other communication patterns, including workers communicating with each other.

Not all parallel algorithms are best implemented using the master-worker model. In computational science, where many algorithms exhibit data parallelism, the Single Program Multiple Data (SPMD) programming model is very suitable (see my notes on GPU Programming with Julia). The message passing interface (MPI) library is the dominant programming model in computational science because of its support for SPMD programming and for its implementation with highly optimized interprocess communication. A subset of the MPI interface is available to Julia programmers in the MPI.jl package.

Computational science programs make heavy use of arrays. Julia supports distributed parallel programming with arrays in the DistributedArrays package.

---