2 Starting out with Racket
\(\newcommand{\la}{\lambda} \newcommand{\Ga}{\Gamma} \newcommand{\ra}{\rightarrow} \newcommand{\Ra}{\Rightarrow} \newcommand{\La}{\Leftarrow} \newcommand{\tl}{\triangleleft} \newcommand{\ir}[3]{\displaystyle\frac{#2}{#3}~{\textstyle #1}}\)
Racket is a functional programming language, which emphasizes the definition of functions and their use. To gain a deeper understanding of the implications of this design, we start with a close reading of how this is done in mathematics, and then translate the concepts over to Racket.
2.1 Functions in mathematics
Here are two simple mathematical definitions.
\begin{align*}f(x)&=x^2\\ g(x,y)&=x+y\\\end{align*}
\(f\) is a function that squares, and \(g\) is a function that adds. In practice, we probably wouldn’t need to name these functions, since we already have ways of denoting these actions, as seen on the right-hand side of each definition. Don’t be misled by simple first examples; the point is to illuminate, not to be representative.
These two definitions are similarly structured. First comes the name of the function, \(f\) and \(g\) respectively. The name of the function is followed by names for the parameters of the function, separated by commas and enclosed in parentheses.
Next is an equal sign \(=\), which should be interpreted as the phrase "is defined to be". The equal sign is followed by the body of the function, which is an expression that uses the argument names.
Once these definitions have been made, we can use or apply these functions to specific arguments, as in the following example.
\begin{align*}g(1,3) &= 1+3\\ &= 4\end{align*}
The expression \(g(1,3)\) means that the first parameter of \(g\) (which has been given the name \(x\) in the definition) should have the value 1, and the second parameter (named \(y\)) should have the value 3. To compute the value of \(g(1,3)\), we substitute 1 for \(x\) and 3 for \(y\) in the body expression \(x + y\) from the definition of \(g\), giving the expression \(1+3\). We then evaluate this according to our understanding of addition, to get the result 4.
We can nest function applications, leading to more complicated expressions like \(g(g(1,3),f(2))\). In this case we have a choice of the order of substitution and evaluation. Here is one ordering.
\begin{align*}g(g(1,3),f(2))&=g(4,f(2))\\ &=g(4,4)\\ &=4+4\\ &=8\\\end{align*}
And here is a different ordering.
\begin{align*}g(g(1,3),f(2)) &= g(1,3)+f(2) \\ &= 4 + f(2) \\ &= 4 + 4\\ &= 8\end{align*}
The order of evaluation does not matter here (the result is the same) but in Racket, when we add other language features, it can make a difference. We will have rules specifying the order of evaluation.
2.2 Function application in Racket
The effect of function application in Racket is the same as in mathematics, but the syntax (the way we form the expression) is different. Racket has a simple, uniform syntax, whose advantages will slowly become evident, but it can be off-putting at first.
In a Racket function application, the name of the function follows the open parenthesis instead of preceding it, and arguments are separated by spaces instead of commas.
\(g(1,3)\) becomes, in Racket, (g 1 3).
\(g(g(1,3),f(2))\) becomes (g (g 1 3) (f 2)).
In arithmetic expressions, we often place operators between their operands, as in the example \(3-2+4/5\). In contrast, with function application, the name of the function comes before its arguments. Schoolchildren have to memorize a set of rules to specify the order of evaluation when reducing such expressions (for example, division before addition, or left to right evaluation). Sometimes these rules do not suffice, and parentheses are required for grouping, as in the example \((6-4)/(5+7)\).
We could use function notation for an operation such as \(+\), treating it as a named function instead of an operator. \(3-2+4/5\) would become \(+(-(3,2),/(4,5))\). Now parentheses are only used to associate arguments with operations, as they are no longer needed for ordering.
This is what is done in Racket. Operators in mathematics become functions in Racket. Parentheses are used only to associate arguments with operations. Ordering of operations is handled by nesting.
\(3-2+4/5\) becomes (+ (- 3 2) (/ 4 5))
\((6-4)(3+2)\) becomes (* (- 6 4) (+ 3 2))
(Notice that the name of the multiplication function is * instead of \(\times\), a historical choice because of the symbols available in early computer character sets.)
Any arithmetic expression can be treated in this fashion, and then converted into a Racket expression. But one must remember to not add extra parentheses. Extra parentheses are harmless in arithmetic expressions, but they will lead to problems in Racket. Only use parentheses when necessary (to signal a function application or some other Racket syntax).
We have only started to learn about the syntax of Racket, but we now know enough for the simplest of interactions with the software itself.
2.3 DrRacket’s Interactions window
If you have not already done so, install Racket from https://www.racket-lang.org, and open the DrRacket application. Racket is actually a family of languages, and it will prompt you to choose one; choose the Beginning Student Language (BSL). This is the lowest of a series of languages designed for learning. They provide small but still powerful subsets of features, which permits clearer error messages.
Full documentation on Racket is available on the Racket web page, but if you have installed Racket, there is a local copy on your computer. If you choose "Racket Documentation" from the Help menu, the local copy will open in your default browser and give you a top-level set of links. For now, you will want to focus on the information about Beginning Student. This can be found under "How To Design Programs languages". It’s easy to stray into the full documentation (especially if you use a Web search engine) but that is likely to be more confusing than helpful until you know more about Racket.
DrRacket will display two windows stacked vertically, called Definitions and Interactions respectively. We will focus on the bottom one, Interactions, for now. This provides a read-evaluate-print loop (REPL). A prompt looking like this: > signals that it is waiting for user input. You can type in expressions and have them evaluated.
> (+ (* 3 3) (* 4 4)) 25
Racket, unlike most programming languages, represents rational numbers exactly, with unbounded precision.
> (/ (expt 6 40) (expt 2 90)) 10798.17609466798060768866207581595517694950103759765625
Some operations produce inexact numbers or complex numbers:
> (sqrt 2) #i1.4142135623730951
> (sqrt -9) 0+3i
Inexact numbers are fixed-precision rational approximations. They are produced when the result of an operation cannot be represented exactly as a rational number, as with the square root of 2. We will not be using them in FICS, but they have their uses, especially in scientific computation (e.g. physical simulations where the position of an object acting under forces is repeatedly updated, and maintaining exact precision might lead to absurd and unnecessary numbers of digits). Similarly, we will not be using complex numbers, but you may enjoy experimenting with them.
So far, the Interactions window seems like a powerful but somewhat awkward calculator. When we add the ability to define our own functions, things get more interesting. We’ll step away from the software for a moment and discuss principles first.
(* (5) 3)
(+ (* 2 4)
(5 * 14)
(* + 3 5 2)
(/ 25 0)
\(\blacksquare\)
2.4 Function definitions in Racket
We can directly translate our examples of defining functions in mathematics into Racket definitions.
\(f(x)=x^2\) becomes (define (f x) (* x x)).
\(g(x,y)=x+y\) becomes (define (g x y) (+ x y))
define is a form (something that looks like a Racket function application, because of the use of parentheses, but which is treated differently). You can see that a Racket program is going to have a lot of parentheses. The editor in DrRacket has features to help us deal with them. For example, if you put the cursor before an open parenthesis, the following expression is highlighted up to the matching close parenthesis.
As with our mathematical definitions, a Racket function definition has a name for the function, a list of parameters, and a single body expression. The body expression typically uses the parameters together with other predefined and user-defined functions. We say that define binds a name to an expression (which uses the parameters that follow the name), and call the result a binding.
An application of a user-defined Racket function substitutes argument values for the corresponding parameters in the definition’s body expression. (g 3 5) is rewritten as (+ 3 5), which evaluates to 8. As hinted at earlier, we need some rules to choose an order of evaluation. We make progress in evaluation by finding a subexpression that is ready for reduction, namely a function application all of whose arguments are values. For example, in the expression (* (- 6 4) (+ 3 2)), there are two such subexpressions, (- 6 4) and (+ 3 2).
Given any two subexpressions of an expression, either one is to the left of the other, or one is contained within the other. Our rule is: choose the leftmost, outermost subexpression that is ready for reduction.
We can visualize each step of the process using the \(\Rightarrow\) symbol, which we can pronounce as "yields".
\(\Rightarrow\) (* 2 5)
\(\Rightarrow\) 10
This mirrors how we work with mathematical expressions, but removes any element of choice in ordering of evaluation. The visualization is for our own mental model of Racket computation. The Interactions window doesn’t show us each step; it just skips ahead to the result. There is a way of seeing each step, which we’ll get to shortly.
The same process works with user-defined Racket functions, using substitution for function application as we described earlier.
(g (g 1 3) (f 2))
\(\Rightarrow\) (g (+ 1 3) (f 2))
\(\Rightarrow\) (g 4 (f 2))
\(\Rightarrow\) (g 4 (* 2 2))
\(\Rightarrow\) (g 4 4)
\(\Rightarrow\) (+ 4 4)
\(\Rightarrow\) 8
We can reuse parameter names in different functions, since each parameter name has a specific meaning only within the body of its function.
| (define (f x y) |
| (+ x y)) |
| (define (g z x) |
| (* x z)) |
The two uses of x are independent. The word we use for this is scope. The scope of a parameter name (where that particular name has that particular meaning) is the body of its function. Scope is an important concept in Racket and will come up again.
In addition to defining functions in Racket, we can also define constants. In mathematics, we might say "Let \(k=3\)". In Racket, this becomes (define k 3). Similarly, "Then let \(p=k^2\)" becomes (define p (* k k)).
The effect of (define k 3) is to bind the name k to the value 3. In (define p (* k k)), the expression (* k k) is first evaluated to give 9, and then p is bound to that value.
In the body of a function, a parameter name shadows a constant of the same name. That is, the scope of the name of a constant is from the point of the definition on, except where the name is also used as the name of a parameter (in which case a use of the name in the body of that function refers to the parameter and not the constant).
| (define x 3) |
| (define (f x y) (- x y)) |
(+ x x) \(\Rightarrow\) 6
(f 7 6) \(\Rightarrow\) 1
(f 5 x) \(\Rightarrow\) (f 5 3) \(\Rightarrow\) (- 5 3) \(\Rightarrow\) 2
It might seem a little superfluous to define a constant, since we can just use the value to which the name is bound. But it can make programs easier to understand. We can give meaningful names to useful values (for example, interest-rate, passing-grade, and starting-salary). It can reduce typing and errors when such values need to be changed.
Constants can be used in any expression, including the body of function definitions. They are sometimes called variables, but their values cannot be changed. The word "variable" is also sometimes used to refer to the use of a parameter name within the body of a function. In this case, there can be actual variation, because the function can be applied to different arguments.
2.5 DrRacket’s Definitions window
Although definitions of functions and constants can be typed into the Interactions window, it makes more sense to put them in the Definitions window, which provides a fully-featured editor with the ability to save the current program and restore it. Expressions can also be entered into the Definitions window, but they are not evaluated immediately. A Racket program, then, is a sequence of possibly intermingled definitions and expressions.
The evaluation process can be triggered with the Run button in the top right corner. This goes through the definitions and expressions in the Definitions window in order. Each definition brings a new name into scope. Each expression is evaluated and the result printed in the Interactions window. Once the whole Definitions window has been processed, all bindings remaining in scope are available in the Interactions window for further experimentation.
The Check Syntax button will check the syntax of the program without running it. As was the case in the Interactions window, expressions are highlighted if the cursor is placed before an open parenthesis or after a close parenthesis. If there is an error during evaluation, an error message will be printed in the Interactions window and the source of the error will be highlighted in the Definitions window.
Finally, the Step button at top right will open a Stepper window in which the step-by-step visualization of expression evaluation that we discussed above can be animated. This can be useful in understanding new computational features as we introduce them. Resist the temptation to use it to fix errors in your programs. We will discuss better techniques for that.
2.6 More types of data
The Boolean data type has two values, #true and #false. Racket also predefines the constants true and false bound to their respective values.
Racket provides many predefined Boolean functions (for example, to do comparisons). Evaluating (= x y) is equivalent to determining whether the mathematical proposition "\(x=y\)" is true or false. In order to determine whether the proposition "\(x < y\)" is true or false, we can evaluate (< x y). There are also functions for \(>\), \(\le\) (written <= ) and \(\ge\) (written >=).
Racket provides the function not and the forms and, or for computation on Boolean values (these consume Boolean values, and produce a Boolean value). They can be used to test complex relationships. The proposition "\(3 \le x < 7\)", which is the same as "\(x \in [3,7)\)", can be computationally tested by evaluating (and (<= 3 x) (< x 7)).
The Racket forms and and or can have two or more arguments. The form and has value #true exactly when all of its arguments have value #true. The form or has value #true exactly when at least one of its arguments has value #true. The function not has value #true exactly when its one argument has value #false.
DrRacket only evaluates as many arguments of and and or as is necessary to determine the value. This is why they are forms and not functions (all arguments of functions are always evaluated). This behaviour can simplify some expressions, as in the following examples.
| (and (not (= x 0)) (<= (/ y x) c)) |
| (or (= x 0) (> (/ y x) c)) |
Evaluation of these expressions will never divide by zero, regardless of the values of x and y. Can you see why?
Exercise 1: Predict the result of evaluating the following expressions, and then check your prediction using DrRacket.
| (not (and (= 1 2) (> 3 1))) |
| (or (not (> 3 2)) (and (< 1 2) (> 2 1))) |
\(\blacksquare\)
Exercise 2: For each of the following expressions, describe the circumstances (if any) under which evaluation of it would result in a divide-by-zero error.
| (or (= x 0) (< 0 (/ y x))) |
| (or (< 0 (/ y x)) (= x 0)) |
| (and (= x 0) (< 0 (/ y x))) |
| (or (< 0 (/ y x)) (not (= x 0))) |
Racket provides a number of predefined predicates (functions producing a Boolean value) such as even?, negative?, and zero?. We can write our own predicates, as in the following examples.
| (define (between? low high numb) |
| (and (< low numb) (< numb high))) |
| (define (can-drink? age) |
| (>= age 19)) |
Here I have split the definitions onto two lines and indented the body expression. This is standard style. One can put a Racket program, even a long one, onto a single line, or onto as many lines as possible by putting each "word" or parenthesis on a separate line. Obviously these extremes are to be avoided, but there still is a lot of room to vary things in two dimensions. Judicious use of spacing and indentation can improve readability. Watch for these stylistic touches as we start to write more complex programs.
I’ll quickly mention two other data types which I’ll initially mostly use to vary examples. Strings are sequences of characters surrounded by double quotes, such as "A Functional Introduction To Computer Science". These are obviously useful for representing and manipulating text, and later in the course we’ll examine techniques for doing so. Symbols resemble strings with some spelling restrictions (they cannot contain spaces, for example), and are represented with a single close quote at the front, such as 'Computer and 'Science. About the only thing one can do with symbols is compare them for equality (which can typically be done quicker than with strings). The utility of symbols will gradually become evident. We will be using them a lot more than you might expect from this brief description.
Speaking of equality, nearly all built-in data types have an equality predicate. We’ve seen = for numbers. For strings, we can use string=?, and for symbols, there is symbol=?. (Ending a predicate with a question mark is also a stylistic convention.) The general purpose predicate equal? tests any two values for equality, regardless of their types. The main reason to use the more specialized equality predicates is that they will signal an error if applied to a value of the wrong type.
2.7 Conditional expressions
Boolean predicates allow us to test for various conditions, but we would also like to vary our computations based on the results of those tests. For example, consider the mathematical definition of a function that computes the maximum of its two numerical arguments.
\[\mathit{max}(x,y) = \begin{cases}x & \mbox{when }x > y \\ y & \mbox{otherwise}\end{cases}\]
We can use the if form to compute this. The form has three arguments. If the first one evaluates to true, the value of the if form is the second argument, otherwise it is the third argument. Note that only one of the second and third arguments is actually evaluated. Here is a Racket function that computes the maximum of the variables x and y:
| (define (my-max x y) |
| (if (> x y) x y)) |
I have named this function my-max because there is a predefined function max which does the same thing (and more, because max can be applied to more than two arguments).
Complex conditions become awkward to write using if, so the more general cond special form is preferred. A use of cond specifies a number of question-answer pairs.
| (cond |
| [question1 answer1] |
| [question2 answer2] |
| ... |
| [questionk answerk]) |
The questions are expressions that are evaluated in order. When one of the questions evaluates to #true, the corresponding answer is evaluated and becomes the value of the cond expression; in this case, none of the remaining questions are evaluated. Only one answer is ever evaluated.
The last question can be else, which, if reached, makes the last (corresponding) answer the value of the cond expression. If there is no else, and none of the questions evaluate to #true, evaluation stops and an error message is printed in the Interactions window. Here is the function above, rewritten using cond:
| (define (my-max x y) |
| (cond |
| [(> x y) x] |
| [else y])) |
Note the use of square brackets and the indentation and spacing. These are stylistic conventions for readability. Square brackets and round parentheses are interchangeable in Racket, except that they must be properly nested (that is, the type of open/close pairs must match). We tend to reserve square brackets for specific situations where they improve readability. Even though the second function definition is longer than the first one, the definition using cond is more readable. You should nearly always use cond in your programs, though you may occasionally find that a tiny if expression is appropriate.
Conditional expressions written using if and cond are expressions that evaluate to a value. They can appear anywhere that a Racket value or other Racket expression might be used. (In some programming languages, conditional statements do not produce a useful value, and cannot be used the same way.)
Exercise 3: Write cond expressions equivalent to the following Boolean expressions.
| (and x y) |
| (or x y z) |
| (not x) |
\(\blacksquare\)
Sometimes a question can be simplified by knowing that if it is asked, all previous questions have evaluated to #false. Suppose our analysis identifies three intervals:
negative numbers,
non-negative numbers less than 100,
numbers greater than or equal to 100.
We might write the tests for the three intervals this way:
| (cond |
| [(< x 0) (f1 x)] |
| [(and (>= x 0)(< x 100)) (f2 x)] |
| [(>= x 100) (f3 x)]) |
In this case, we can simplify the second and third tests.
| (cond |
| [(< x 0) (f1 x)] |
| [(< x 100) (f2 x)] |
| [else (f3 x)]) |
These simplifications become second nature with practice.
Conditional expressions greatly expand the power of Racket, and we are almost ready to start writing some interesting programs. But before we do so, let’s put some good habits in place that will pay off when things get complex.
2.8 The design recipe
When I taught this material in courses, I would tell my students that if I had to choose only one slide for them to remember, it would be the one that contained only the following paragraph.
Between you and the computer
Between you and yourself in the future
Between you and others
It’s too easy to focus on using a program to accomplish a task. But a program is also the most accurate description of how the task is accomplished. We should do what we can to make it easier for ourselves or others to extend or modify our programs.
Internal documentation is part of this. Racket, like most programming languages, allows embedded comments that are for human readers only. Anything from a semicolon (;) to the end of the line it is on will be ignored when the program is run. DrRacket displays such comments in a different colour.
Both comments and the programs they are commenting on should be developed in a structured manner. The design recipe from the How To Design Programs (HtDP) textbook is a development process that leaves behind written explanation of the development, and results in a trusted (tested) function which future readers can understand. It is a software engineering methodology aimed at beginners but which is still useful for experts.
HtDP starts with five design recipe components, and adds more as new ways of computing are introduced.
Contract: Describes what type of arguments the function consumes and what type of value it produces.
Purpose: Describes what the function is to compute.
Examples: Illustrating the use of the function.
Definition: The Racket definition (header and body) of the function.
Tests: A representative set of function applications and expected values.
To illustrate these components, we’ll write a function which squares two numbers and sums the results. Of course, a function this simple doesn’t need a design methodology, but once again, a simple first example is best.
In mathematics, we might describe the function this way:
sum-of-squares: \(\mathbb{R}\times \mathbb{R} \rightarrow \mathbb{R}\)
That is, the function, called "sum-of-squares", consumes two real numbers and produces a real number. (We could restrict the domain and range to natural numbers, or integers, or expand it to complex numbers.)
Here is the result of using the design recipe to write the Racket function.
| ; sum-of-squares: Number Number -> Number |
| ; Purpose: produces sum of squares |
| ; of arg1 and arg2 |
| ; Examples: |
| (check-expect (sum-of-squares 3 4) 25) |
| (check-expect (sum-of-squares 0 2.5) 6.25) |
| (define (sum-of-squares arg1 arg2) |
| (+ (* arg1 arg1) (* arg2 arg2))) |
There are a number of things that I need to explain here, notably the use of check-expect in the examples, but I’ll do that from top to bottom, starting with the contract. We adapt the idea of the mathematical description, with a typographical approximation of a right arrow between the types of the arguments and the type of the result. Since this is a comment, we have some latitude in describing the types. By convention, we’ll use the following names for types in contracts.
Number: any Racket numeric value
Int: restriction to integers
Nat: restriction to natural numbers (including 0)
Any: any Racket value
We will see more types soon.
The code for the Racket function definition consists of the header (name of function and parameters) and the body (a Racket expression using parameters). The header should be written earlier than the purpose, and the body written later. The purpose can then use the parameter names in such a way as to make their meaning clear.
Examples should be written earlier than the body. The examples can then serve as a guide to writing the body.
Tests should be written later than the code body. They can then address complexities encountered while writing the body. Tests don’t need to be "big". In fact, they should be small and directed. The number of tests and examples needed is a matter of judgement, and will become more clear with some experience.
Since you are reading these words voluntarily, free of the need to earn marks, I don’t expect you to fall into some of the traps that my students sometimes do when working hastily under time pressure. But just in case old habits die hard, it should be clear, on reflection, that one should not figure out the expected answers to one’s tests by running one’s program. Always work them out by hand.
| (check-expect (sum-of-squares 3 4) 25) |
| (check-within (sqrt 2) 1.414 0.001) |
| (check-error (/ 1 0) |
| "/: division by zero") |
The check-expect form consumes two arguments, an expression which is usually an application of the function being written to specific arguments, and an expected value. check-within adds a third argument, an error tolerance, for use with inexact numbers. Finally, check-error replaces the second argument with the exact text of an error message.
Tests written using these forms are saved and evaluated at the very end of the program. This means that examples can be written as code, without running into problems because the examples appear before the definition. DrRacket will either say "All tests passed!" in the Interactions window, or will pop up an error window with details of which tests failed and how. Because it is so simple to write tests and deal with failing ones, the system encourages writing many tests. This is good, because our tendency usually is to avoid testing, or to write too few tests.
When we add a couple of tests, here is the finished program.
; sum-of-squares: Number Number -> Number ; Purpose: produces sum of squares ; of arg1 and arg2 ; Examples: (check-expect (sum-of-squares 3 4) 25) (check-expect (sum-of-squares 0 2.5) 6.25) (define (sum-of-squares arg1 arg2) (+ (* arg1 arg1) (* arg2 arg2))) (check-expect (sum-of-squares 0 0) 0) (check-expect (sum-of-squares -2 7) 53)
A couple of examples and a couple of tests is about the right number for a function this simple. A more complicated arithmetic computation might demand a few more.
Tests get more complicated when conditional expressions are used in the code. You should include at least one test for each possible answer in the expression. That test should be simple and direct, aimed at testing that answer by satisfying the corresponding question (and none of the prior ones) in as straightforward a manner as possible.
Often tests are appropriate at boundary points as well. Here is our three-interval example again.
| (cond |
| [(< x 0) (f1 x)] |
| [(< x 100) (f2 x)] |
| [else (f3 x)]) |
There are three intervals and two boundary points, so five tests are required (for instance, x could take on the values -10, 0, 10, 100, 150).
Testing and and or expressions is similar. For (and (not (zero? x)) (<= (/ y x) c)), we need:
one test case where \(x\) is zero (first argument to and is false, so the value of the whole expression is false, and the other arguments are not evaluated)
one test case where \(x\) is nonzero and \(y/x > c\), (first argument to and is true, so the second argument is evaluated, and it is false)
one test case where \(x\) is nonzero and \(y/x \le c\). (first argument to and is true, so the second argument is evaluated, and it is true)
Some of your tests, including your examples, will have been defined before the body of the function was written. These are known as black-box tests, because they are not based on details of the code. Other tests may depend on the code, for example, to check specific answers in conditional expressions. These are known as white-box tests. Both types of tests are important.
In the interests of brevity, I will not always include all components of the design recipe in the examples here, but you should use it when you do the exercises.
2.9 An extended example
There’s an old saying: "Nothing is certain but death and taxes". Of the two, I prefer taxes, and that will be the subject of this example. Canada has a progressive income tax system: the rate of tax increases with income. In 2021, the rates were:
no tax payable on negative income
15% from $0 up to $49,020
22% from $49,020 up to $98,040
26% from $98,040 up to $151,978
29% from $151,978 up to $216,511
33% above $216,511
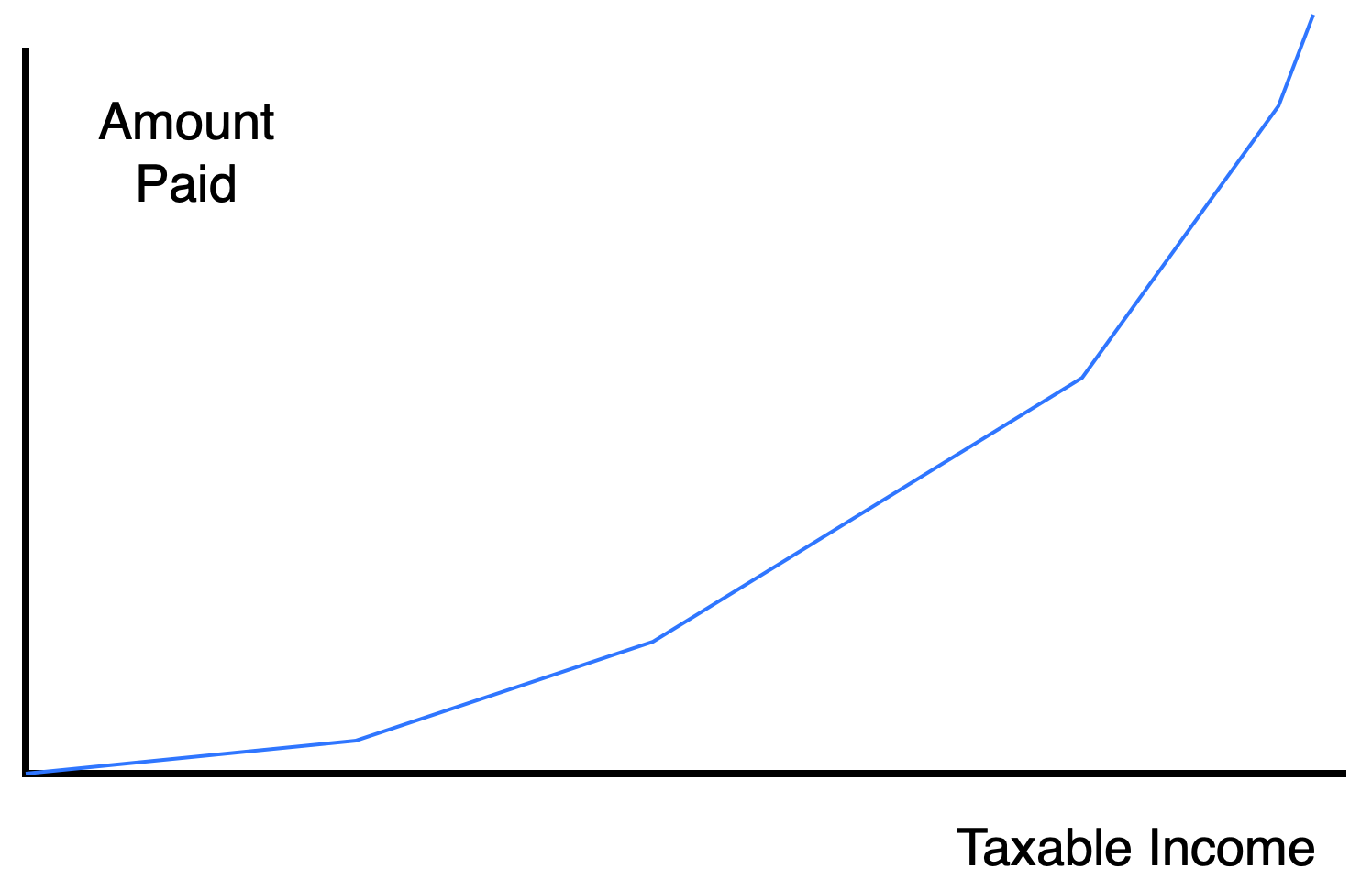
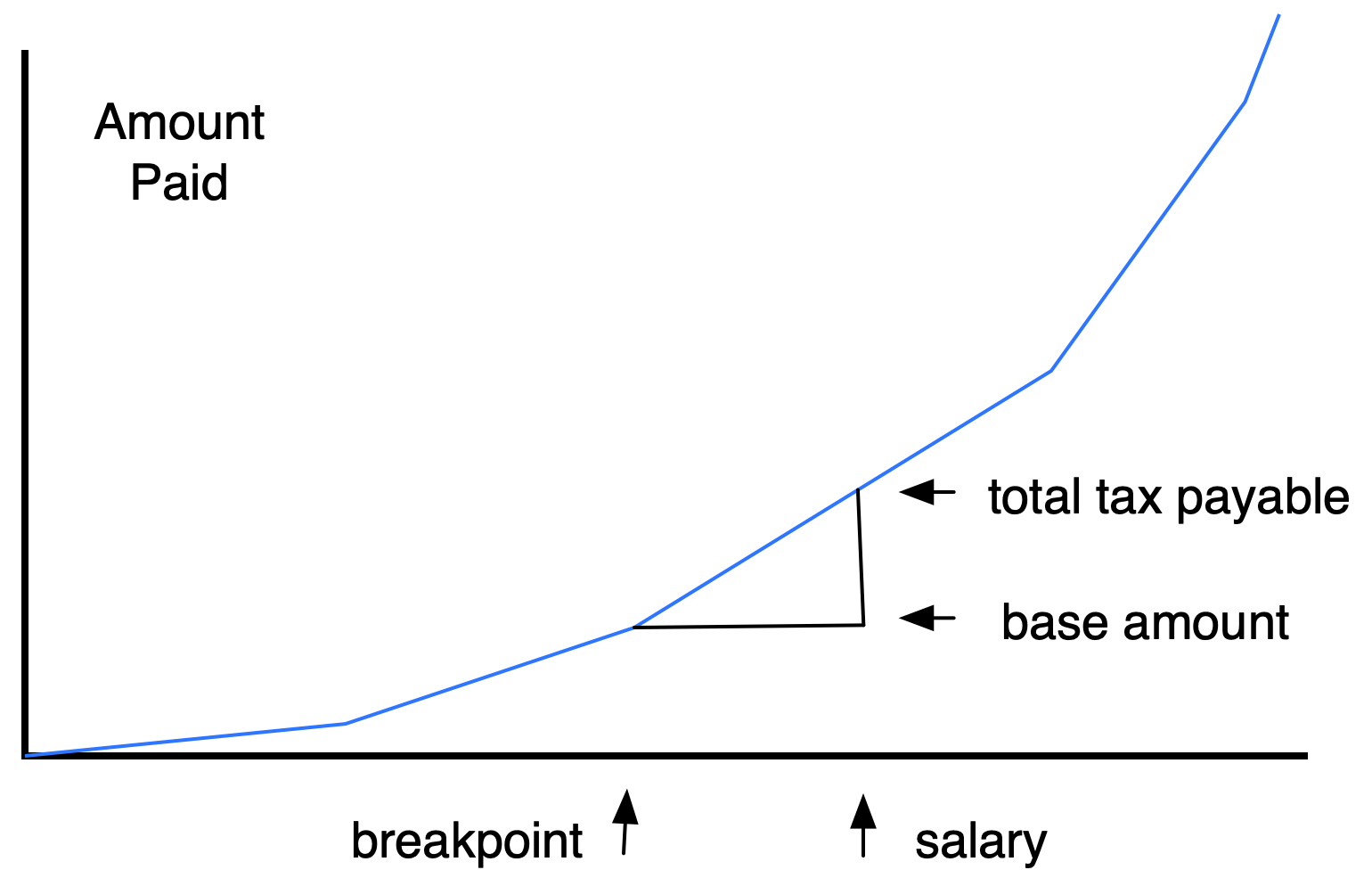
The piecewise linear nature of the graph complicates the computation of tax payable. One way to do it uses the breakpoints (\(x\)-value or salary when the rate changes) and base amounts (\(y\)-value or tax payable at breakpoints). This is what the paper Canadian tax form does.
We create defined constants for breakpoints and rates in the Racket program.
| ; breakpoints |
| (define bp1 49020) |
| (define bp2 98040) |
| (define bp3 151978) |
| (define bp4 216511) |
| ; rates |
| (define rate1 0.15) |
| (define rate2 0.205) |
| (define rate3 0.26) |
| (define rate4 0.29) |
| (define rate5 0.33) |
Instead of putting the base amounts into the program as numbers (as the tax form does), we can compute them from the breakpoints and rates. We use a conditional expression to find the largest breakpoint smaller than or equal to the salary, and then compute the incremental tax to be added to the corresponding base amount as the difference between the salary and that breakpoint, multiplied by the corresponding tax rate.
| ; basei is the base amount |
| ; for interval [bpi,bp(i+1)] |
| ; that is, tax payable at income bpi |
| (define base1 (* bp1 rate1)) |
| (define base2 (+ base1 (* (- bp2 bp1) rate2))) |
| (define base3 (+ base2 (* (- bp3 bp2) rate3))) |
| (define base4 (+ base3 (* (- bp4 bp3) rate4))) |
| (define (tax-payable income) |
| (cond |
| [(<= income 0) 0] |
| [(<= income bp1) (* income rate1)] |
| [(<= income bp2) (+ base1 (* (- income bp1) rate2))] |
| [(<= income bp3) (+ base2 (* (- income bp2) rate3))] |
| [(<= income bp4) (+ base3 (* (- income bp3) rate4))] |
| [else (+ base3 (* (- income bp3) rate4))])) |
There are many similar calculations in the tax program, leading to the definition of the following helper function to handle them all.
| (define (tax-calc base low high rate) |
| (+ base (* (- high low) rate))) |
This can be used both in the definition of constants and in the main function.
| (define base1 (tax-calc 0 0 bp1 rate1)) |
| (define base2 (tax-calc base1 bp1 bp2 rate2)) |
| (define base3 (tax-calc base2 bp2 bp3 rate3)) |
| (define base4 (tax-calc base3 bp3 bp4 rate4)) |
| (define (tax-payable income) |
| (cond |
| [(<= income 0) 0] |
| [(<= income bp1) (tax-calc 0 0 income rate1)] |
| [(<= income bp2) (tax-calc base1 bp1 income rate2)] |
| [(<= income bp3) (tax-calc base2 bp2 income rate3)] |
| [(<= income bp4) (tax-calc base3 bp3 income rate4)] |
| [else (tax-calc base3 bp3 income rate4)])) |
Helper functions generalize similar expressions, and can be used to avoid long, unreadable function definitions. A functional programming language such as Racket encourages us to use helper functions. You should use your judgement on how many to include. Don’t go overboard, but sometimes even very short definitions can improve readability.
Except for a helper function that basically renames another function, you should use the design recipe. For example, among the examples and tests for tax-payable, we could use the base amounts from the official form to check our computation of the defined constants.
Exercise 4: Write the Racket function middle-of-three that consumes three numbers and produces the number that would be between the other two if they were listed in non-decreasing order. As an example, (middle-of-three 1 3 2) should produce 2. \(\blacksquare\)
Exercise 5: Write the function interval-proper-subset? that consumes four numbers. The first two represent a closed interval on the real number line and the second two another closed interval; for instance, the four numbers 4.5 5.5 2 6 represent the two intervals \([4.5,5.5]\) and \([2,6]\). You may assume that the number describing the left endpoint of each interval is less than or equal to the number describing the right endpoint.
The function produces true if and only if the set of points in the first interval is a subset of the set of points contained in the second interval, but not equal to it (this being the definition of a proper subset). In our example, the first interval is a proper subset of the second interval, so the result of evaluating (interval-proper-subset? 4.5 5.5 2 6) would be true. \(\blacksquare\)
It may seem as though I’ve been quite precise in describing Racket syntax and computation. In the following chapter, I’ll be even more precise, and in the process, will introduce more foundational concepts of computer science.