Important information
- the test will be Friday October 21 in class.
Practice questions
1. transforms
2D
Give an example in 2D that shows that scaling and rotations are not always commutative.
3D
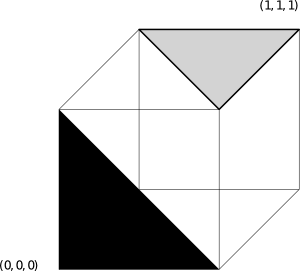
Give a transformation matrix that maps the black triangle to the gray one. You may leave your answer as a product of matrices, with rotations given symbolically as e.g. Rz(45) meaning rotate CCW 45 degrees about the z axis.
2. Camera Coordinates
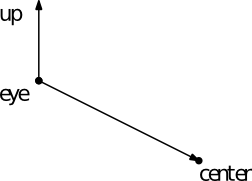
Explain how to compute the view matrix give the eye position, the up vector, and the point center being looked at.
3. Projection matrices
Example projection/depth transform matrix
Consider the matrix
P =
1 0 0 0
0 1 0 0
0 0 3 -2
0 0 1 0
Describe the effect of the matrix, both geometrically and in the context of a rendering pipeline.
Describe the effect of applying this transformation twice.
Perspective projection matrix
Give a matrix that implements the following perspective transformation (D is the distance to the near clipping plane). Explain your answer.
[x,y,z,w]ᵀ → [Dx/z, Dy/z, D]
4. Clipping
Give robust inequlities to clip a homogeneous point [x,y,z,w]ᵀ
against the standard cube [-1,1]×[-1,1]×[-1,1]. Are there any special
cases? If so, explain.